people have died from curable diseases

since this page started loading...

💀

Wishocracy: Solving the Democratic Principal-Agent Problem Through Pairwise Preference Aggregation

Representative democracy suffers from an inescapable principal-agent problem where elected officials’ incentives diverge from citizen welfare. Wishocracy introduces RAPPA (Randomized Aggregated Pairwise Preference Allocation), which aggregates citizen preferences through cognitively tractable pairwise comparisons and creates accountability via Citizen Alignment Scores that channel electoral resources toward politicians who actually represent what citizens want.

Author

Affiliation

Mike P. Sinn

Decentralized Institutes of Health

Doi

10.5281/zenodo.18205882

Keywords

mechanism design, principal-agent problem, collective intelligence, direct democracy, preference aggregation, participatory budgeting, analytic hierarchy process, public resource allocation

Version 0.9 - Working Draft

Seeking peer review and contributions. If you have expertise in voting theory, preference aggregation, participatory governance, or behavioral economics, your feedback and potential co-authorship would be greatly valued. Please annotate via the sidebar or contact [email protected].

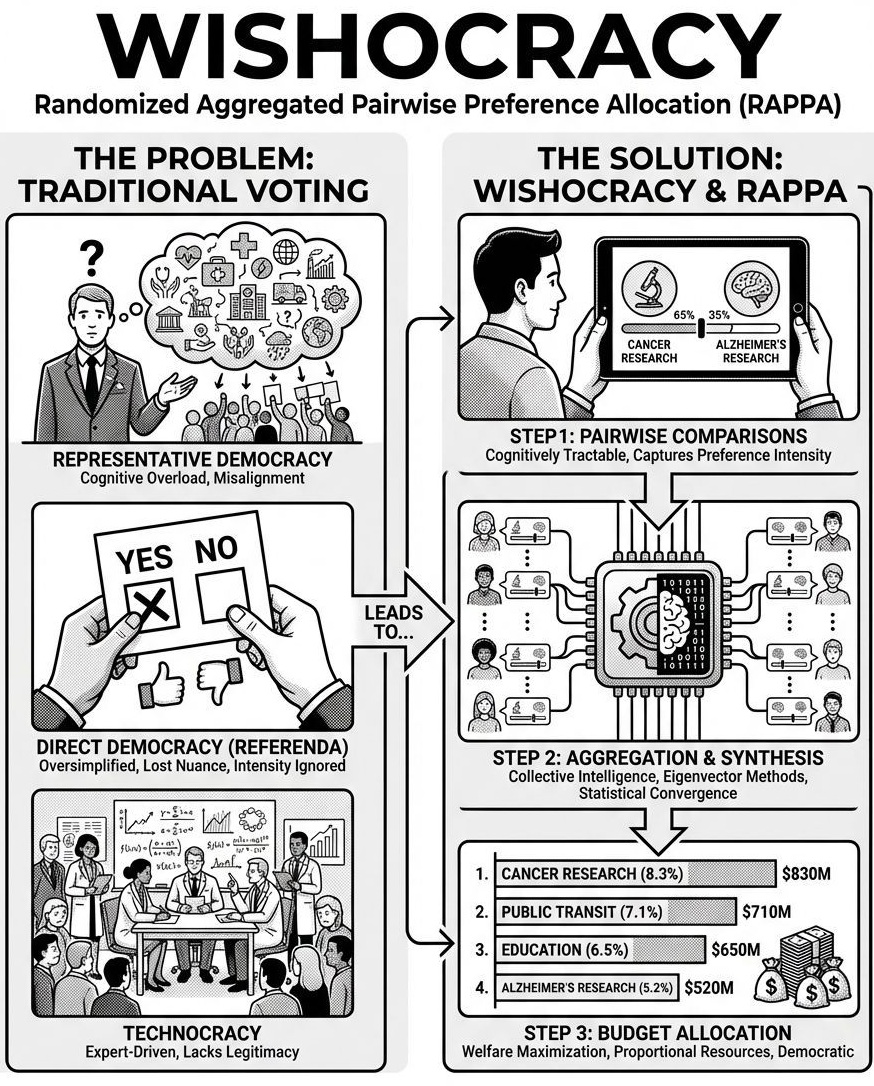
The Problem in One Sentence: Representative democracy suffers from an inescapable principal-agent problem: elected officials face incentives (re-election, donor pressure, special interests) that systematically diverge from citizen welfare, while direct democracy mechanisms are too cognitively demanding to scale beyond binary referenda.

The Solution: Wishocracy aggregates citizen preferences through simple pairwise comparisons (‘allocate $100 between cancer research and military spending’) and creates accountability for elected officials by publishing how their voting records align with these preferences. This channels electoral and financial resources toward politicians who actually represent what citizens want.

1 Abstract

Representative democracy suffers from a fundamental principal-agent problem: elected officials systematically diverge from citizen preferences due to information asymmetry, special interest capture, and misaligned incentives. Meanwhile, direct democracy mechanisms reduce complex trade-offs to binary choices, losing crucial information about preference intensity. This paper introduces Wishocracy, a governance mechanism that addresses the democratic principal-agent problem by aggregating citizen preferences and creating accountability for elected representatives. The mechanism employs Randomized Aggregated Pairwise Preference Allocation (RAPPA), which presents participants with simple pairwise comparisons (‘allocate $100 between cancer research and infrastructure’) and aggregates millions of such judgments into preference weights that approximate utilitarian social welfare. Building on the Analytic Hierarchy Process² for cognitive tractability and collective intelligence research³ for aggregation, RAPPA decomposes n-dimensional preference spaces into tractable binary choices while preserving preference intensity information. We present formal mechanism properties, computational complexity analysis, and empirical precedents from Porto Alegre’s participatory budgeting, Taiwan’s vTaiwan platform, and Stanford’s voting research. Rather than replacing representative democracy at the municipal level, we propose a federal-first implementation: (1) documenting the gap between citizen preferences and actual federal allocations, (2) creating public “Citizen Alignment Scores” for elected officials, and (3) integrating with Incentive Alignment Bonds to channel electoral and financial resources toward politicians whose voting records align with aggregated citizen preferences. This approach treats Wishocracy as an accountability mechanism that makes representative democracy work better, requiring no authority transfer, only information provision and incentive alignment.

2 Introduction: The Preference Aggregation Problem

Modern democracies face an increasingly acute challenge: how to translate the diverse, often conflicting preferences of millions of citizens into coherent public policy. Traditional electoral mechanisms were designed for an era of limited communication, discrete choices, and relatively homogeneous electorates. Today’s policy landscape (spanning healthcare allocation, infrastructure investment, climate adaptation, research funding, and social services) demands more sophisticated preference elicitation than periodic elections can provide.

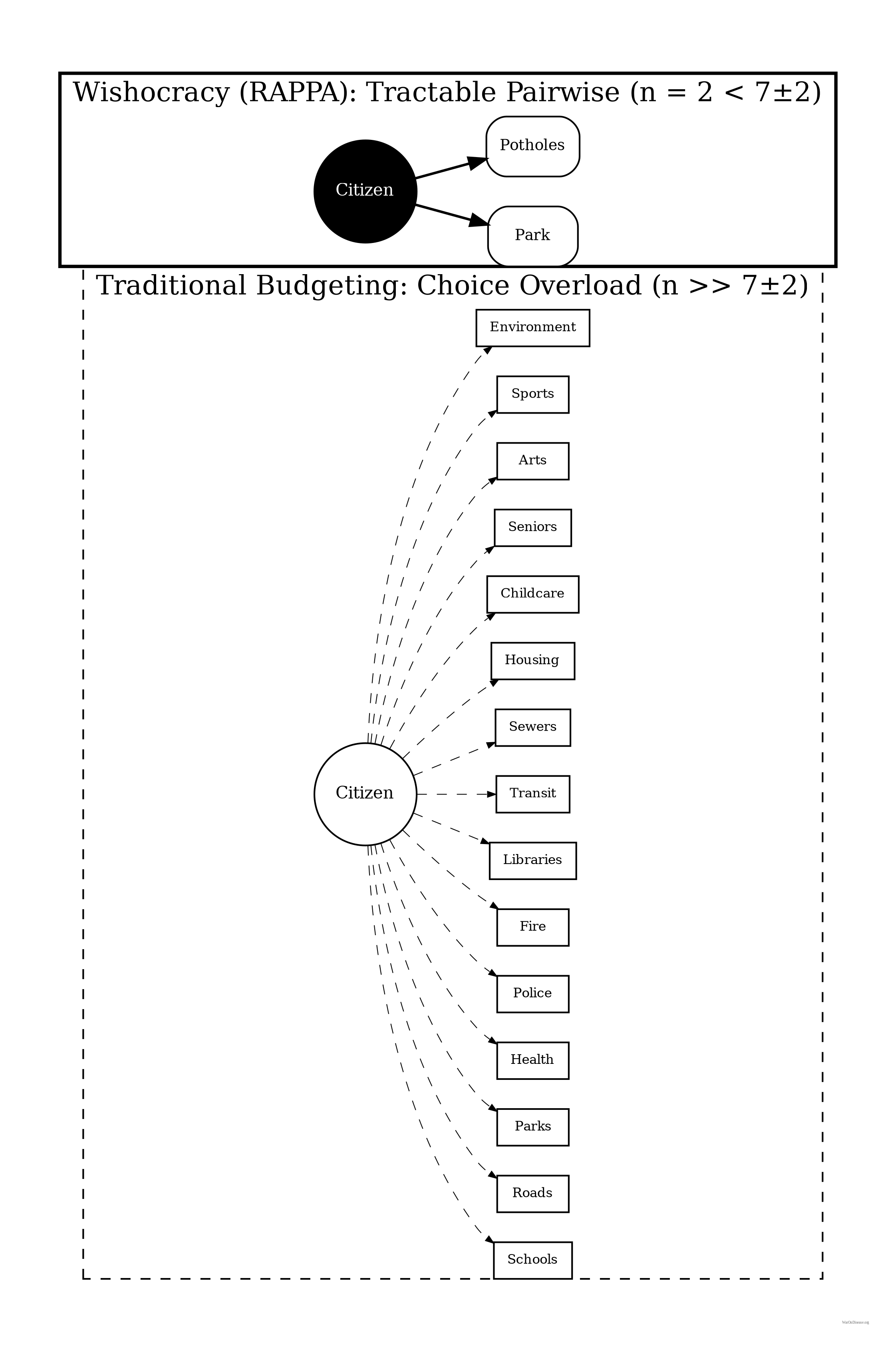
The fundamental problem is computational and cognitive. When citizens are asked to rank or rate dozens of competing priorities simultaneously, they face impossible cognitive demands. Research in behavioral economics has consistently demonstrated that humans cannot reliably compare more than 7±2 options simultaneously⁴. Humans struggle to make consistent judgments over large sets of options. Pairwise comparisons keep each decision local and cognitively manageable even when the full budget has thousands of items.

Yet modern government budgets allocate resources across thousands of line items, each representing implicit trade-offs against all others.

Figure 1: Cognitive Load Comparison: Direct Ranking vs. RAPPA. Assessing many items simultaneously exceeds human working memory ($7 \pm 2$). RAPPA decomposes this into a sequence of binary choices, keeping cognitive load low.

Existing solutions fall into three inadequate categories. First, representative democracy delegates preference aggregation to elected officials, introducing principal-agent problems, capture by special interests, and systematic misalignment between voter preferences and policy outcomes. Second, direct democracy mechanisms like referenda and citizen initiatives reduce complex trade-offs to binary choices, losing crucial information about preference intensity and creating winner-take-all dynamics that harm minorities with strong preferences. Third, expert-driven technocracy may achieve allocative efficiency but lacks democratic legitimacy and cannot incorporate the subjective welfare considerations that only citizens themselves can evaluate.

Wishocracy offers a fourth path: a mechanism that harnesses collective intelligence through structured preference elicitation while respecting cognitive constraints, incorporating preference intensity, and maintaining democratic legitimacy. By presenting citizens with simple pairwise comparisons (‘Given $100 to allocate between cancer research and Alzheimer’s research, how would you divide it?’), the mechanism decomposes the impossible n-dimensional comparison into tractable binary choices. Aggregated across millions of such comparisons from thousands of participants, the system converges on a preference ordering that approximates the utilitarian social welfare function under stated assumptions.

RAPPA’s Contribution: Wishocracy synthesizes four properties into a single framework:

Cognitive Tractability: By decomposing n-dimensional budget allocation into pairwise comparisons (drawing on AHP), RAPPA respects the well-documented cognitive limit of $7 \pm 2$ simultaneous comparisons, making participation feasible for all citizens regardless of education or available time.
Cardinal Preference Intensity: Through slider-based allocation between pairs, participants reveal not just ordinal rankings but the strength of their preferences, allowing the mechanism to weight both the number of supporters and the intensity of their support.
Collective Intelligence Aggregation: By synthesizing millions of pairwise judgments through eigenvector methods, the mechanism uses diversity to cancel individual errors while aggregating true signals into allocations that approximate utilitarian social welfare.
Accountability Integration: By producing clear, quantifiable preference signals that can be compared against politician voting records, RAPPA enables accountability mechanisms (Citizen Alignment Scores, Incentive Alignment Bonds) that align representative behavior with citizen welfare.

To our knowledge, no widely deployed mechanism combines all four properties. Traditional voting captures neither intensity nor tractability. The Analytic Hierarchy Process provides tractability but has been deployed primarily for expert decision-making, not large-scale collective governance. Existing accountability mechanisms (interest group scorecards) reflect narrow priorities rather than aggregated citizen preferences. RAPPA synthesizes insights from decision science and collective intelligence to enable genuine democratic accountability.

3 Theoretical Foundations

3.1 The Analytic Hierarchy Process

Wishocracy’s methodological core derives from the Analytic Hierarchy Process (AHP), developed by Thomas Saaty at the Wharton School in the 1970s. AHP has been extensively validated across thousands of applications in business, engineering, healthcare, and government⁵. The method works because humans can reliably make pairwise comparisons even when direct multi-attribute rating fails.

AHP works by decomposing complex decisions into hierarchies of criteria and sub-criteria, then eliciting pairwise comparisons at each level. For n alternatives, this requires only n(n-1)/2 comparisons rather than the cognitively impossible simultaneous comparison of all n options. The pairwise comparison matrices are then synthesized using eigenvector methods to produce consistent priority rankings.

Crucially, AHP includes consistency checks through the calculation of a Consistency Ratio (CR). When individual judgments violate transitivity (e.g., A > B, B > C, but C > A), the method flags these inconsistencies for review. In Wishocracy’s collective aggregation, individual inconsistencies cancel out through the law of large numbers, while systematic collective preferences emerge from the aggregate.

3.2 The Preference Intensity Problem

A fundamental limitation of traditional voting is the failure to account for preference intensity. Under one-person-one-vote, a citizen who mildly prefers policy A has equal influence to one for whom policy A is existentially important. This leads to systematic welfare losses: intense minorities can be steamrolled by indifferent majorities, and the resulting allocations fail to maximize aggregate welfare.

Several mechanisms have attempted to address this problem. Quadratic voting⁶ allows voters to purchase additional votes at quadratic cost, approaching efficiency as the number of voters grows. The Colorado House Democratic Caucus used QV in 2019 to prioritize legislative priorities. However, QV imposes significant cognitive burden: participants must manage vote budgets across many issues simultaneously, understand quadratic cost structures, and make strategic decisions about where to spend limited credits.

RAPPA takes a different approach: pairwise slider allocation captures preference intensity naturally without requiring participants to understand any cost function or manage budgets. When a participant allocates 90% to cancer research and 10% to Alzheimer’s research, they express strong preference intensity. A 55-45 split signals near-indifference. This information emerges from intuitive trade-off judgments rather than strategic budget management. Aggregated across the population, these intensity signals produce allocations that weight both the number of supporters and the strength of their preferences, achieving the welfare benefits of intensity-weighted voting without the cognitive overhead.

3.3 Collective Intelligence and the Wisdom of Crowds

Wishocracy’s aggregation mechanism relies on the well-documented phenomenon of collective intelligence.³ synthesized research showing that diverse, independent groups consistently outperform individual experts under four conditions: diversity of opinion, independence of judgment, decentralization of information, and effective aggregation mechanisms.

Randomized pairwise presentation ensures independence by preventing any systematic ordering effects. Diversity is maximized by including all citizens rather than restricting participation to experts or stakeholders. Decentralization emerges naturally from distributed participation. Wishocracy provides the crucial aggregation mechanism that previous collective intelligence applications have lacked.

Page’s diversity prediction theorem formalizes this intuition: collective error equals average individual error minus diversity. A diverse crowd makes different mistakes that cancel out, while sharing enough common knowledge that true signals aggregate. Wishocracy’s slider allocation (rather than binary choice) increases the information content per comparison, improving convergence rates.

3.4 Related Work and Positioning in the Literature

RAPPA exists within a broader landscape of democratic innovation and participatory governance mechanisms. We position Wishocracy relative to four major alternative approaches:

Liquid Democracy: Liquid democracy allows voters to either vote directly on issues or delegate their voting power to trusted representatives, with the ability to revoke delegation at any time. Examples include DelegativeVoting and Google’s internal Liquid Feedback experiments. While liquid democracy addresses representation flexibility, it does not solve the cognitive load problem: delegates still face the impossible task of ranking dozens of policy priorities simultaneously. RAPPA complements liquid democracy by providing a tractable preference elicitation method that delegates (or direct voters) can use.

Futarchy: Proposed by economist Robin Hanson, futarchy uses prediction markets to aggregate information about which policies will best achieve agreed-upon goals. Under futarchy, “vote on values, bet on beliefs”: citizens determine welfare metrics democratically, then prediction markets determine which policies maximize those metrics. Futarchy excels at aggregating distributed information about causal mechanisms but assumes consensus on welfare metrics. RAPPA addresses the complementary problem: eliciting and aggregating preferences over competing welfare priorities when citizens disagree about relative importance (e.g., cancer research vs. education funding).

Conviction Voting: Used in decentralized autonomous organizations (DAOs), conviction voting allows continuous preference expression where tokens “accumulate conviction” on proposals over time. This mechanism rewards patience and sustained support while preventing sudden swings. However, conviction voting typically applies to binary proposal approval (fund this project: yes/no) rather than continuous budget allocation across competing priorities. RAPPA’s pairwise comparison approach enables proportional allocation that reflects both preference intensity and relative prioritization.

Participatory Budgeting: Traditional participatory budgeting (as pioneered in Porto Alegre⁷ and discussed in Section 4.1) involves citizen assemblies deliberating on budget proposals, followed by voting⁸. While highly democratic, this approach faces scalability limits: participation rates typically remain under 5%, and cognitive load increases exponentially with the number of budget items⁹. RAPPA retains participatory budgeting’s democratic legitimacy while achieving scalability through decomposition and statistical aggregation.

Comparative Advantages: RAPPA’s unique contribution lies in simultaneously addressing three constraints that limit alternative mechanisms: (1) Cognitive tractability through pairwise decomposition, (2) Preference intensity capture through slider-based allocation, and (3) Scalable aggregation through eigenvector methods that synthesize sparse distributed inputs. Where liquid democracy addresses who decides, futarchy addresses how to predict outcomes, and conviction voting addresses temporal aggregation, RAPPA addresses how to elicit preferences over complex multidimensional spaces.

This positioning suggests natural complementarities: RAPPA could serve as the preference elicitation layer for liquid democracy delegates, provide the “vote on values” component for futarchy systems, or replace binary voting in conviction voting contexts where proportional allocation is needed.

4 Mechanism Design: Randomized Aggregated Pairwise Preference Allocation

4.1 Core Mechanism

The Wishocracy mechanism operates through the following process, which we term Randomized Aggregated Pairwise Preference Allocation (RAPPA):

Problem Cataloging: A comprehensive list of societal priorities, problems, or ‘wishes’ is compiled through expert input, citizen submissions, or existing government planning documents. These might include ‘Reduce cancer mortality,’ ‘Improve public transit,’ ‘Increase affordable housing,’ etc.
Randomized Pair Presentation: Each participant is shown a series of randomly selected pairs from the problem catalog. For each pair, they are asked: ‘Given $100 to allocate between these two priorities, how would you divide it?’ A slider interface allows allocation anywhere from 100-0 to 0-100.
Aggregation: All pairwise allocations are aggregated across participants. For each pair (A, B), the system calculates the mean allocation ratio. If participants on average allocate 65% to A and 35% to B, this establishes the relative priority weight.
Matrix Completion: Using the aggregated pairwise ratios, a complete preference matrix is constructed. Standard eigenvector methods (as in AHP) or iterative Bayesian updating produce global priority weights for all n items.
Budget Allocation: The final priority weights translate directly into budget allocation percentages. If cancer research receives a normalized weight of 8.3% and the total discretionary budget is $10 billion, cancer research receives $830 million.

4.1.1 Scenario: Federal Budget Preferences

Imagine Citizen Alice opening the Wishocracy app to express her preferences on federal spending.

Comparison 1: She is presented with a pair: “Medical Research (NIH)” vs. “Military Weapons Systems”.
Decision: Alice lost her mother to Alzheimer’s and believes medical research is severely underfunded. She slides the allocator to give 85% to Medical Research and 15% to Military. This expresses strong intensity.
Comparison 2: Next, she sees “Military Weapons Systems” vs. “Drug Enforcement (DEA)”. She thinks both receive more than they should but slightly prefers maintaining military capability. She allocates 60% to Military and 40% to Drug Enforcement.
Aggregation: Millions of other citizens make similar pairwise comparisons. Alice never sees “Medical Research vs. Drug Enforcement,” but the system infers the relationship (Medical Research > Military > Drug Enforcement) through the transitive network of all citizens’ choices.
Result: The aggregate preferences reveal that citizens would allocate significantly more to medical research and less to military and drug enforcement than Congress currently does. This “Preference Gap” becomes the basis for Citizen Alignment Scores: politicians who vote to increase NIH funding score higher; those who vote for military expansion despite citizen preferences score lower.

4.2 Formal Properties

RAPPA satisfies several desirable mechanism design properties:

Pareto-Respecting (Discussion): The mechanism aims to produce allocations where no reallocation could make some participants better off without making others worse off, though formal proof depends on specific utility assumptions.

Manipulation Resistance: Random pair assignment makes strategic manipulation difficult. A participant cannot know which pairs they will receive, making truthful reporting a robust heuristic. With sufficiently large participant pools, individual strategic behavior has negligible impact on outcomes.

Cognitive Tractability: Each individual comparison requires only binary evaluation with an intensity slider, well within human cognitive capacity. Participants need not understand the aggregation mathematics.

Scalability: The number of pairwise comparisons grows quadratically with items (n²/2), but each participant need only complete a small random sample. Statistical convergence requires far fewer total comparisons than exhaustive coverage.

Preference Intensity Capture: Unlike binary voting, the slider allocation captures cardinal preferences. Strong majorities with weak preferences can be outweighed by smaller groups with intense preferences, addressing the tyranny of the majority problem.

Comparative Mechanism Complexity: The table below summarizes how RAPPA compares to alternative voting mechanisms across key dimensions:

Mechanism	Comparisons per participant	Cognitive load	Intensity capture	Strategy-proofness
Traditional voting (plurality)	O(1)	Minimal	No	No
Ranked-choice (RCV)	O(n log n)	High	No	Partial
Quadratic voting (QV)	O(n)	Medium-high	Yes	Partial
RAPPA	O(k) where k << n	Minimal	Yes	Approximate

To our knowledge, widely deployed mechanisms do not simultaneously optimize for these three properties at civic scale.

4.3 Formal Model

We now formally define the RAPPA mechanism as a mapping from individual preferences to collective allocations.

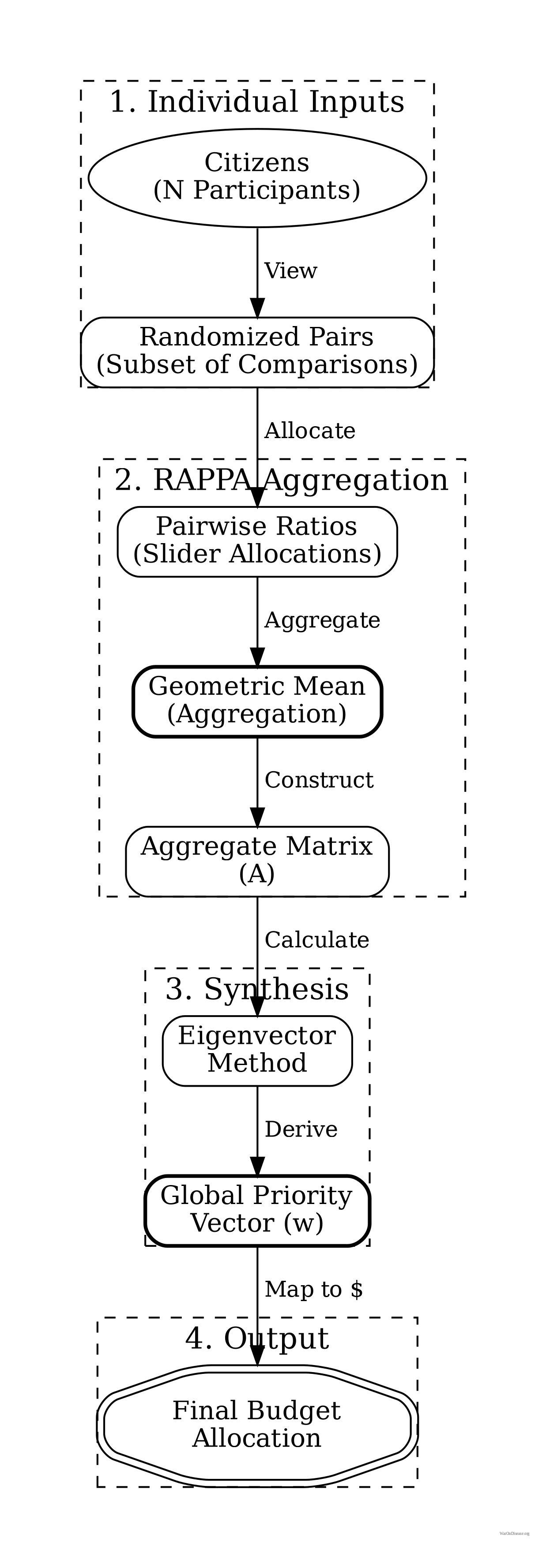
Inputs: Let $N = \{1, ..., n\}$ be the set of citizens and $O = \{o_1, ..., o_m\}$ be the set of policy priorities. Each citizen $i$ provides pairwise allocation ratios $\rho_{i,A,B} \in [0,1]$ for a subset of pairs $(A,B) \in O \times O$.

Ratio Conversion: The raw slider value $\rho$ (a share) is converted into a preference odds ratio $r$ (unbounded $[0, \infty)$) to satisfy AHP requirements. We apply $\epsilon$-clipping to handle edge cases (0/100): \[ r_{i,A,B} = \frac{\rho_{i,A,B} + \epsilon}{1 - \rho_{i,A,B} + \epsilon} \] where $\epsilon$ is a small constant (e.g., $10^{-3}$) to prevent singularities.

Aggregation Function: For each pair $(o_j, o_k)$, we compute the aggregate pairwise comparison using the Geometric Mean of individual odds ratios (following¹⁰, which proves geometric mean is necessary to preserve the reciprocal property in pairwise comparisons): \[ a_{jk} = \left( \prod_{i \in S_{jk}} r_{i,j,k} \right)^{\frac{1}{|S_{jk}|}} \]

Note: While we use geometric mean to aggregate individual pairwise comparisons (to preserve reciprocity), the resulting eigenvector priority weights approximate the arithmetic mean of individual utilities under appropriate conditions (see² for details). where $S_{jk} \subseteq N$ is the set of citizens who evaluated the pair. This produces a sparse $m \times m$ comparison matrix $\mathbf{A}$.

Priority Synthesis: We compute priorities from the sparse matrix $\mathbf{A}$. While classical AHP uses the principal eigenvector of a dense matrix, for sparse data we employ logarithmic least squares (LLSM) or iterative methods to recover the global priority vector $\mathbf{w} = (w_1, ..., w_m)^T$ such that $a_{jk} \approx w_j / w_k$.

Output: The final budget allocation assigns fraction $w_j$ of total resources to priority $o_j$.

Welfare Justification: Under quasi-linear preferences where citizen $i$’s utility from allocation $\mathbf{x} = (x_1, ..., x_m)$ is $u_i(\mathbf{x}) = \sum_{j=1}^{m} v_{ij} x_j$, the pairwise allocation $\rho_{i,j,k}$ reveals the relative valuations $v_{ij}/v_{ik}$. The eigenvector aggregation produces weights $w_j$ proportional to $\sum_{i \in N} v_{ij}$, thus approximating the utilitarian welfare function $W(\mathbf{x}) = \sum_{i=1}^{n} u_i(\mathbf{x})$ under budget constraint $\sum_{j} x_j = B$.

Convergence Properties: Define the log-odds ratio $y_{i,jk} = \ln r_{i,j,k}$. With $\epsilon$-clipping, $y$ is bounded in $[\ln \epsilon - \ln(1+\epsilon), \ln(1+\epsilon) - \ln \epsilon]$. The aggregate estimator $\hat{y}_{jk} = \frac{1}{|S_{jk}|} \sum_{i \in S_{jk}} y_{i,jk}$ concentrates around the population mean by Hoeffding’s inequality. The final aggregate ratio is $a_{jk} = \exp(\hat{y}_{jk})$.

Wishocracy implies a separation of concerns: RAPPA determines what society values (the priority vector $\mathbf{w}$), while the implementation of those priorities is handled by a separate layer of competitive problem-solving organizations (see Appendix A: The Solution Layer). This distinction prevents the mechanism from bogging down in technical debates during the preference aggregation phase.

4.4 Computational Complexity and Scalability

We now analyze the computational requirements of RAPPA and establish scalability bounds for real-world deployment.

Comparison Collection Complexity: For $m$ policy priorities, the complete pairwise comparison space contains $\binom{m}{2} = \frac{m(m-1)}{2} = O(m^2)$ unique pairs. However, RAPPA employs random sampling rather than exhaustive coverage. Each of $n$ participants completes $k$ comparisons, yielding total comparison count $T = n \cdot k = O(nk)$. $k$ can be held constant (e.g., $k=20$ comparisons per participant) regardless of $m$, making per-participant complexity $O(1)$ rather than $O(m^2)$.

Aggregation Complexity: Given $T$ collected comparisons distributed across $O(m^2)$ possible pairs, aggregation proceeds in three steps:

Geometric mean calculation: For each observed pair $(j,k)$, compute geometric mean of $|S_{jk}|$ individual ratios¹⁰. Using log transformation: $\ln a_{jk} = \frac{1}{|S_{jk}|} \sum_{i \in S_{jk}} \ln r_{i,j,k}$. Complexity: $O(T)$ for summing all comparisons, then $O(m^2)$ for averaging pairs.
Matrix completion: Convert sparse observations into $m \times m$ matrix $\mathbf{A}$. For dense eigenvector methods (classical AHP²), this requires $O(m^3)$ operations for eigendecomposition. For sparse data, iterative methods (e.g., logarithmic least squares, coordinate descent) converge in $O(m^2 \log m)$ operations given sufficient comparison density.
Priority normalization: Normalize eigenvector to sum to 1. Complexity: $O(m)$.

Total system complexity: $O(nk + m^2 \log m)$ where the first term dominates for large-scale deployments ($n \gg m$).

Scalability Limits: Real-world constraints impose practical bounds:

Policy priorities ($m$): Pilot deployments (municipal budgets): $m = 20-50$ items. State/national budgets: $m = 100-500$ items. Full government budget line items: $m = 5,000-10,000$ items. The $O(m^2 \log m)$ aggregation complexity remains tractable even at $m=10,000$ (requiring ~10^9 operations, feasible on commodity hardware in seconds).
Participants ($n$): Municipal scale: $n = 1,000-10,000$ participants. City scale: $n = 10,000-100,000$. National scale: $n = 1,000,000+$. The linear $O(n)$ scaling in comparison collection makes national-scale deployment computationally feasible.
Comparisons per participant ($k$): Empirical testing at wishocracy.org¹¹ suggests $k=10-30$ comparisons provides good user experience (5-10 minutes) while achieving convergence. Comparison density $\rho = \frac{nk}{m(m-1)/2}$ should exceed $\rho > 0.05$ for reliable estimates, implying minimum $nk > 0.025m^2$ or equivalently $n > 0.025m^2/k$.

Benchmark Example (City-Scale Deployment): Consider a city budget with $m=100$ priorities, $n=50,000$ participants, $k=20$ comparisons each:

Total comparisons: $T = 50,000 \times 20 = 1,000,000$
Comparison density: $\rho = \frac{1,000,000}{100 \times 99 / 2} = \frac{1,000,000}{4,950} \approx 202$ (highly overdetermined)
Aggregation time: $O(100^2 \log 100) \approx 66,000$ operations (milliseconds on modern hardware)
Storage: $O(m^2) = 10,000$ matrix entries (kilobytes)

This analysis demonstrates that RAPPA scales efficiently to city and even national deployments with commodity computing infrastructure. The sparse, distributed nature of data collection combined with efficient matrix completion algorithms makes the mechanism computationally tractable across all realistic governance scales.

Empirical Performance: The reference implementation at wishocracy.org¹¹ processes 10,000 comparisons across 50 items in under 100ms on standard cloud infrastructure (AWS t3.medium instance). Extrapolating linearly, national-scale deployment (1M participants, 100 items) would require ~10 seconds of aggregation time, negligible compared to voting/deliberation timescales measured in days or weeks.

4.5 Comparative Information & Welfare Analysis

We now formally demonstrate the superiority of RAPPA over Representative Democracy (RepDem) using Information Theory and Social Choice Theory. We model governance as an optimization process where the objective is to minimize the divergence between the distribution of societal needs (preferences) and the distribution of resource allocation.

4.5.1 Information-Theoretic Superiority

Governance can be modeled as a source coding problem. Let $\mathcal{P}$ be the true distribution of societal preferences over $m$ issues. The mechanism must encode $\mathcal{P}$ into a signal transmitted to the allocation engine.

Representative Democracy (Low-Bandwidth Channel):

In RepDem, a voter transmits a single scalar signal $v \in \{c_1, \dots, c_k\}$ (choosing one of $k$ candidates) every $T$ years. The channel capacity $C_{Rep}$ is severely limited by quantization noise. A voter with a precise preference vector $\vec{p} \in \mathbb{R}^m$ must compress this into a single nominal vote. \[ C_{Rep} \approx \frac{\log_2(k)}{T \text{ years}} \approx 0 \] This extreme lossy compression effectively destroys all information about preference intensity and specific trade-offs (The “Bundle Problem”). This theoretical result aligns with empirical findings by¹², who analyzed 1,779 policy outcomes and found that “average citizens have little or no independent influence” on policy.

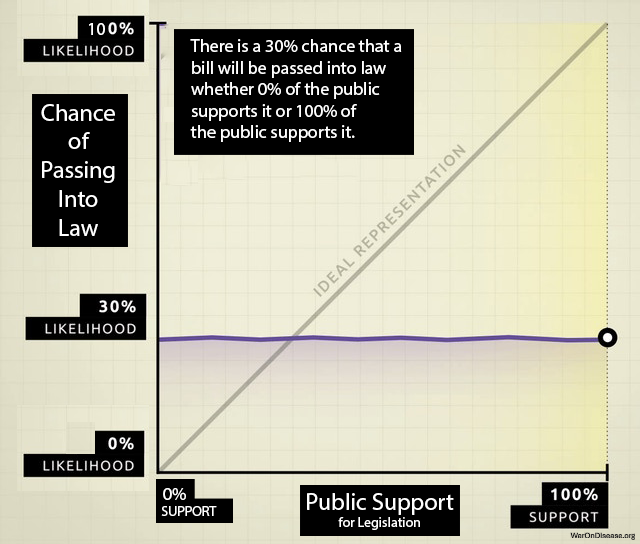
The flatline of democracy: Public support (0% to 100%) has near-zero impact on the probability of policy adoption (flat at ~30%), whereas elite support strongly correlates with adoption. Data from¹².

Wishocracy (High-Bandwidth Channel):

RAPPA operates as a continuous channel. Each pairwise comparison extracts $\log_2(\text{resolution})$ bits of information about the relative valuation of outcome bundle subsets. With continuous sliders, the transmission rate is limited only by citizen engagement time. \[ C_{RAPPA} \propto N \cdot \bar{c} \cdot H(S) \] where $N$ is voters, $\bar{c}$ is average comparisons per voter, and $H(S)$ is the entropy of the slider input.

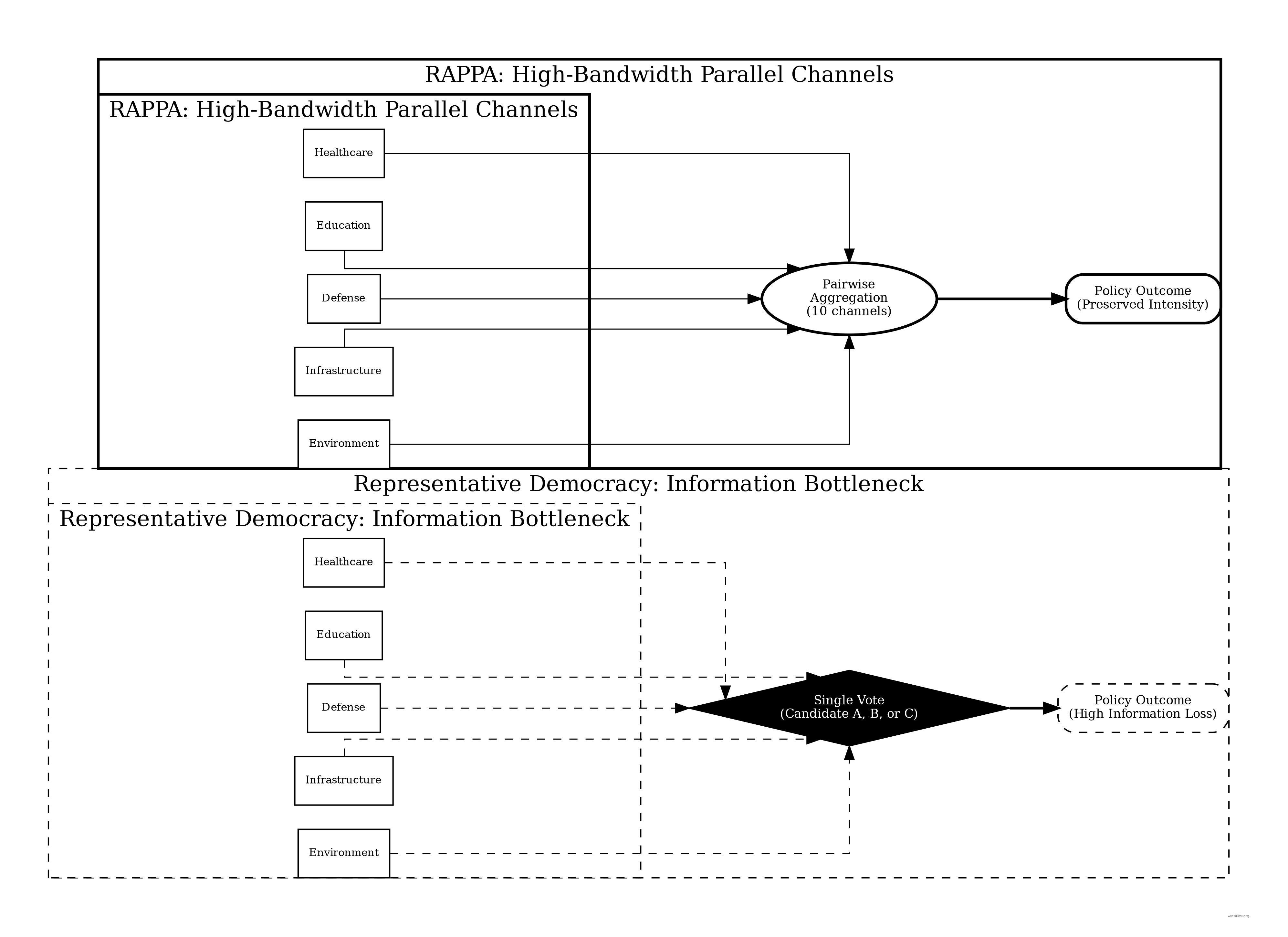
Figure 2: Information Flow Comparison: Representative Democracy vs. RAPPA. RepDem compresses rich preference spaces into a single vote (severe information loss). RAPPA maintains high bandwidth through parallel pairwise channels, preserving preference intensity and trade-off information.

Proposition 1 (Information Loss in Candidate Voting): Let $D_{KL}(P || Q)$ be the Kullback-Leibler divergence between true welfare preferences $P$ and enacted policy $Q$. As $N \to \infty$: \[ E[D_{KL}(P || Q_{RAPPA})] \ll E[D_{KL}(P || Q_{Rep})] \] Argument (Sketch): By the Data Processing Inequality, post-processing (policymaking) cannot increase information. $Q_{Rep}$ is derived from a signal with near-zero mutual information $I(P; V_{Rep})$ due to quantization. $Q_{RAPPA}$ is derived from a sufficient statistic of the pairwise matrix $\mathbf{A}$, where $I(P; \mathbf{A})$ approaches $H(P)$ as empirical sampling density increases.

4.5.2 Welfare Maximization: The “Median vs. Mean” Proof

A fundamental result in Public Choice Theory is the Median Voter Theorem¹³, which states that under majority rule, outcomes converge to the preferences of the median voter, $v_{median}$.

The Skewness Problem: In healthcare and public risk, damage distributions are highly right-skewed (power laws). A few citizens suffer catastrophic loss (e.g., rare diseases, pandemics), while the majority experiences zero loss.

Median Outcome: If 51% of voters have priority $x=0$ (healthy) and 49% have priority $x=100$ (dying), the median preference is $0$. The minority receives no aid.
Mean Outcome: The utilitarian optimum is $\bar{x} = 0.49 \times 100 = 49$.

Proposition 2 (Tail-Risk Under Median Aggregation): For any utility distribution $U$ with skewness $\gamma > 0$ (typical of health/wealth distributions), the Social Welfare $W$ of the RAPPA allocation exceeds that of the Median Voter allocation. \[ W(RAPPA) \approx W(\text{Mean}) > W(\text{Median}) \] Argument: The RAPPA eigenvector centrality $w_j$ corresponds to $\frac{\sum v_{ij}}{\sum \sum v_{ik}}$, which approximates the population arithmetic mean. For convex loss functions (where distinct needs exist), minimizing the sum of squared errors leads to the mean, not the median. Wishocracy thus passes the “Veil of Ignorance” test¹⁴ whereby a citizen typically prefers the Mean allocation to the Median allocation to hedge against being in the tail risk category.

4.5.3 Principal-Agent Cost Elimination

Total Governance Loss $L_{Gov}$ can be decomposed into Aggregation Loss (failure to aggregate preferences) and Agency Loss (corruption/misalignment).

\[ L_{Gov} = L_{Agg} + L_{Agency} \]

RepDem: suffer from high $L_{Agency}$. Politicians maximize independent utility functions (re-election, donor favoring) rather than $W$. Deviation can be arbitrarily large.

Formally, let the voter’s utility be $U_{voter}(\mathbf{x}) = f(\text{Health}, \text{Wealth}, \text{Security})$ over allocation $\mathbf{x}$. The politician’s utility is:

\[ U_{pol}(\mathbf{x}) = \alpha U_{voter}(\mathbf{x}) + \beta U_{donors}(\mathbf{x}) + \gamma P(\text{ReElection} | \mathbf{x}) \]

where $\beta, \gamma \gg 0$. Since donor interests ($U_{donors}$) often conflict with public welfare ($U_{voter}$) (e.g., lower regulation vs. clean air), and re-election depends on short-term signaling rather than long-term outcomes, $\text{argmax}(U_{pol}) \neq \text{argmax}(U_{voter})$.

Wishocracy: $L_{Agency} \to 0$. The mechanism is direct; there is no agent to bribe.
Constraint: Wishocracy introduces $L_{Coordination}$ (the difficulty of designing solutions), which is why the service provider layer (Appendix A) re-introduces agents only for implementation, not for priority setting, minimizing the scope of potential agency loss to technical execution rather than value judgment.

5 Empirical Precedents and Evidence Base

5.1 Porto Alegre Participatory Budgeting

The closest large-scale precedent for Wishocracy is participatory budgeting (PB), pioneered in Porto Alegre, Brazil in 1989. Under the Workers’ Party administration, citizens were invited to deliberative assemblies to determine municipal investment priorities. By 1997, PB produced remarkable results: sewer and water connections increased from 75% to 98% of households; health and education budgets grew from 13% to 40% of total spending; the number of schools quadrupled; and road construction in poor neighborhoods increased five-fold.

Participation grew from fewer than 1,000 citizens annually in 1990 to over 40,000 by 1999. The World Bank documented PB’s success in improving service delivery to the poor and has since recommended its adoption worldwide. Over 2,700 governments have implemented some form of participatory budgeting.

However, Porto Alegre also illustrates the fragility of participatory mechanisms. When political support waned after 2004, PB was gradually defunded and eventually suspended. This underscores the importance of institutional embedding and legal protection for any participatory mechanism seeking long-term stability.

5.2 Taiwan’s Digital Democracy Experiments

Taiwan’s vTaiwan platform, launched in 2014 by civic hacker Audrey Tang (later Taiwan’s Digital Minister), demonstrates the potential of technology-mediated preference aggregation. The platform used Pol.is, a tool that maps opinions and identifies consensus clusters, to deliberate on contentious policy issues including ridesharing regulation and online alcohol sales.

In the alcohol sales deliberation, approximately 450 citizens participated in pairwise opinion comparisons over several weeks, producing consensus recommendations that resolved a four-year regulatory deadlock. The MIT Technology Review noted that ‘opposing sides had never had a chance to actually interact with each other’s ideas. When they did, it became apparent that both sides were basically willing to give the opposing side what it wanted.’

vTaiwan’s limitations (lack of binding authority, limited scope, and eventual political marginalization) provide crucial lessons. Wishocracy addresses these by proposing integration with actual budget allocation rather than advisory recommendations.

5.3 Stanford Participatory Budgeting Platform Research

Academic research on voting interfaces provides direct evidence for RAPPA’s design choices.¹⁵ compared cumulative voting, quadratic voting, and traditional ranking methods on Stanford’s Participatory Budgeting platform. Their findings support several Wishocracy design principles.

Voters preferred more expressive methods over simple approval voting, even though expressive methods required more cognitive effort. Participants showed ‘strong intuition for outcomes that provide proportional representation and prioritize fairness.’ The Method of Equal Shares voting rule was perceived as fairer than conventional Greedy allocation.

⁹ found that voting input formats using rankings or point distribution provided a ‘stronger sense of engagement in the participatory process.’ These findings validate RAPPA’s slider-based allocation over binary choice mechanisms.

5.4 Colorado Quadratic Voting Experiment

The Democratic caucus of the Colorado House of Representatives conducted a quadratic voting experiment in April 2019 to prioritize legislative priorities among 107 possible bills. Each legislator received 100 virtual tokens to allocate across issues, with costs increasing quadratically.

Results demonstrated that QV produces different outcomes than majority voting. The winning bill (Equal Pay for Equal Work Act) received broad but not universal support with strong preference intensity. No representative spent all tokens on a single bill, suggesting the mechanism successfully encouraged preference diversification.

5.5 Reference Implementation: Wishocracy.org

To validate the technical feasibility of the RAPPA mechanism, a reference implementation has been deployed at Wishocracy.org. This open-source platform serves as a pilot environment for:

Interface Testing: Validating the usability of slider-based pairwise comparisons on mobile and desktop devices.
Algorithm Verification: Testing the convergence properties of the geometric mean aggregation and eigenvector centrality algorithms under real-world traffic.
Sybil Resistance: Implementing and stress-testing integration with decentralized identity providers to ensure one-person-one-vote integrity.

The repository is available for public audit, allowing researchers to verify that the theoretical properties described in Section 3 transform correctly into executable code.

5.5.1 Category Selection and Validation Methodology

The reference implementation uses official federal budget categories drawn from OMB and CBO classifications. Participants see neutral descriptions based on government terminology, not researcher-created labels or value judgments about which programs are “good” or “bad.”

For research validation purposes only (not shown to participants), we track existing benefit-cost ratio estimates from established sources:

Category	External BCR Estimate	Source
Medical Research	45:1	Copenhagen Consensus
Early Childhood Programs	13:1	Heckman Equation
Substance Abuse Treatment	7:1	NIDA
Drug Enforcement	Contested	Various
Energy Subsidies	Contested	IMF, industry groups
Corrections	Contested	Vera Institute, DOJ

These estimates allow researchers to test a key empirical question: Does RAPPA converge toward allocations that maximize estimated social welfare, or do citizen preferences systematically diverge from expert BCR estimates? Either finding is informative. Convergence suggests collective intelligence successfully aggregates welfare-relevant information. Divergence suggests either (a) BCR estimates miss welfare dimensions citizens care about, (b) citizens have information economists lack, or (c) preference aggregation reflects values beyond utilitarian welfare maximization.

BCR estimates are contested and often politically coded. The same program may have “high ROI” according to one source and “negative ROI” according to another. RAPPA does not assume any particular BCR estimate is correct. The mechanism reveals citizen preferences; researchers can then compare those preferences to various expert estimates.

5.5.2 Zero-Funding Filter Optimization

A naive implementation of RAPPA requires $\frac{n(n-1)}{2}$ pairwise comparisons for $n$ categories. For 10 categories, this means 45 pairs per participant (cognitively burdensome and likely to produce survey fatigue).

The reference implementation adds a preliminary question: “Should the government fund [category] at all?” Participants can respond Yes, No, or Unsure. Categories marked “No” are excluded from that participant’s pairwise comparisons.

Complexity reduction: If a participant eliminates $k$ categories, their required comparisons drop from $\frac{n(n-1)}{2}$ to $\frac{(n-k)(n-k-1)}{2}$. For $n=10$ and $k=3$:

\[ \text{Pairs} = \frac{10 \times 9}{2} = 45 \rightarrow \frac{7 \times 6}{2} = 21 \text{ (53\% reduction)} \]

Information preservation: The zero-funding response is itself preference data. A participant who excludes “Nuclear Weapons Modernization” has revealed an extreme preference (0% allocation) that can be incorporated into the aggregation. The mechanism effectively captures both intensive margin preferences (slider allocations between funded categories) and extensive margin preferences (whether to fund at all).

Cognitive benefits: Participants report higher engagement when they feel the comparisons are relevant to their values. Forcing someone who believes drug enforcement should be defunded to repeatedly compare it against other categories produces frustration without additional information.

5.5.3 Hierarchical Category Structure

A fundamental design question is granularity: should RAPPA operate on a flat list of thousands of budget line items, or on a hierarchical structure that mirrors how budgets are actually organized?

Flat structure (thousands of items, sparse sampling): Each participant sees a random subset of pairs from the full item space. With enough participants, the law of large numbers ensures convergence. However, voters cannot have informed opinions on obscure line items (“Naval Air Systems Command Procurement Account 1319”). Aggregating uninformed noise produces meaningless allocations.

Hierarchical structure (category → subcategory → line item): Participants first allocate across high-level categories (Defense, Healthcare, Education, Infrastructure). Those who want to engage further can drill down: Defense → Personnel vs. Procurement vs. R&D; Healthcare → Medicare vs. Medicaid vs. NIH. This matches how AHP was designed. It decomposes complex decisions into hierarchies of criteria and sub-criteria.

The reference implementation uses a hybrid approach:

Required: High-level allocation across ~10-15 major budget functions (using OMB classifications)
Optional: Drill-down within categories of interest
Aggregation: High-level weights determine category budgets; drill-down weights allocate within categories

This structure has several advantages:

Citizens can have informed opinions at the category level
Engaged participants can express fine-grained preferences
Aggregation is tractable (hierarchical eigenvector methods)
Results map directly onto existing budget structures

The tradeoff is that participants who don’t drill down delegate sub-allocation to those who do. If only defense hawks drill down within the Defense category, sub-allocations will skew hawkish even if the population-level Defense allocation is modest. Mitigation: weight drill-down responses by high-level allocation (a participant who allocated 5% to Defense gets less influence on Defense sub-allocation than one who allocated 30%).

5.5.4 Framing Bias and Mitigation

How categories are named, described, and presented can systematically bias outcomes. This is not a hypothetical concern. Decades of survey research demonstrate that framing effects routinely shift responses by 10-30 percentage points.

Sources of framing bias:

Category naming: “Investment in clean energy” vs. “Energy subsidies” vs. “Renewable energy programs” will produce different allocations for identical spending.
Description length: Categories with longer, more detailed descriptions may receive more funding simply because participants understand them better.
Presentation order: Categories shown first or last may receive systematically different allocations.
Anchoring: Showing current spending levels may anchor participants toward the status quo.
Loaded language: “Waste, fraud, and abuse” vs. “Program integrity” describes the same spending.

Mitigation strategies in the reference implementation:

Bias Source	Mitigation
Category naming	Use official OMB/CBO terminology; A/B test alternative phrasings
Description asymmetry	Standardize descriptions to ~25 words with consistent structure
Order effects	Randomize category order for each participant
Anchoring	Option to show/hide current spending (test whether it changes allocations)
Loaded language	Adversarial review by politically diverse panel before deployment

Validation approach: Run parallel surveys with different framings on matched samples. If allocations shift significantly based on framing, that framing is biased and should be revised. The goal is descriptions where reasonable people across the political spectrum agree the language is neutral, even if they disagree on the allocation.

Transparency: All category names, descriptions, and any A/B test results should be publicly documented. If critics can identify biased framing, that’s valuable feedback for improvement.

No framing is perfectly neutral. The choice to include or exclude a category is itself a framing decision. But rigorous attention to framing bias distinguishes legitimate preference aggregation from push polling.

6 Addressing Potential Criticisms

6.1 Participation and Digital Divide

Criticism: Digital participation mechanisms exclude citizens without internet access, technological literacy, or time to participate.

Response: Wishocracy should be deployed as a complement to, not replacement for, existing democratic institutions. Multiple access modalities (smartphone apps, web interfaces, public kiosks at libraries and government offices, and paper-based alternatives) can maximize inclusion. Statistical weighting can correct for demographic participation biases, as routinely done in survey research. The cognitive simplicity of pairwise comparisons (unlike lengthy deliberative processes) makes participation accessible to citizens with limited time or formal education.

6.2 Manipulation and Sybil Attacks

Criticism: Bad actors could create multiple accounts or coordinate voting blocs to manipulate outcomes.

Response: Identity verification through existing government ID systems (driver’s licenses, national ID cards) provides one-person-one-account guarantees. We address manipulation at three levels: individual strategic behavior, coordinated attacks, and formal incentive compatibility.

Individual Strategic Behavior: Consider a citizen evaluating pair $(A, B)$. Under random pair assignment, the citizen does not know: (1) which other pairs they will receive, (2) which pairs other citizens will evaluate, or (3) how others will allocate. This incomplete information structure creates a situation where truthful reporting is a robust heuristic: with random assignment and negligible individual impact, the incentive to game outcomes is weak for most participants. Formally, let $\rho_i$ be citizen $i$’s true valuation ratio and $\hat{\rho}_i$ be their reported ratio for pair $(A,B)$. The citizen’s influence on the final weight $w_A$ is:

\[ \frac{\partial w_A}{\partial \hat{\rho}_i} = \frac{1}{|S_{AB}|} \cdot \frac{\partial w_A}{\partial a_{AB}} \]

where $|S_{AB}|$ is the sample size for pair $(A,B)$. With large $n$, this influence is negligible ($O(1/n)$), making strategic manipulation costly relative to its impact. Moreover, since the citizen cannot predict which of their comparisons will be pivotal, expected utility maximization reduces to truthful reporting across all pairs.

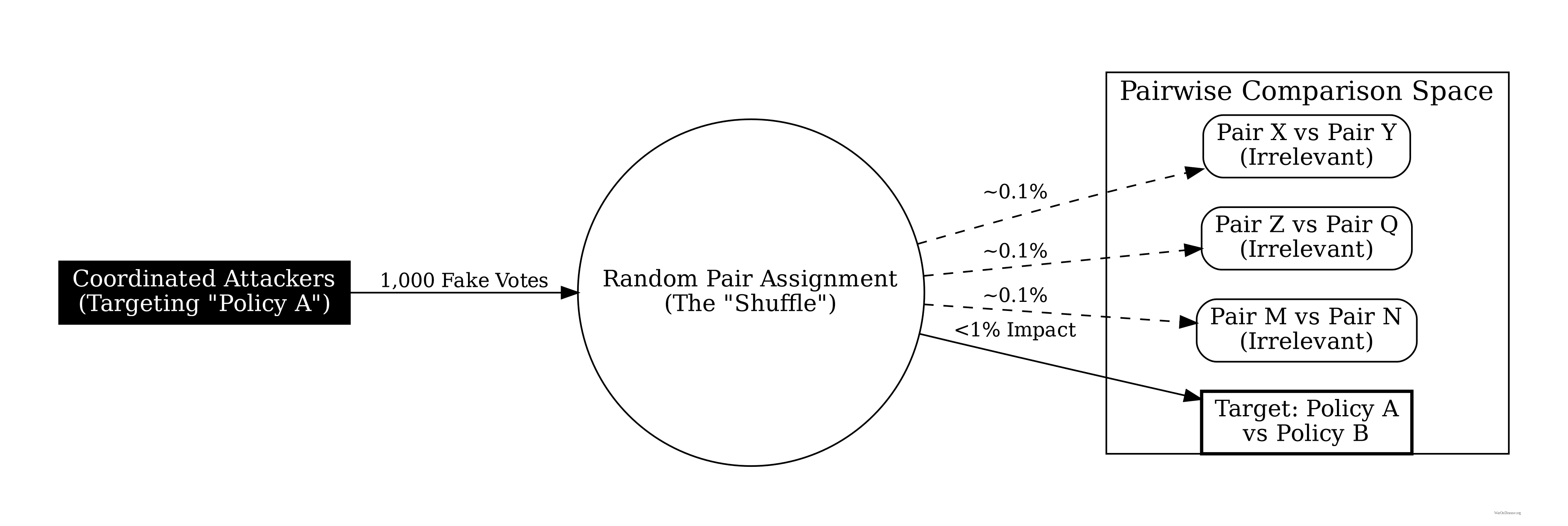
Coordinated Attacks: For a coordinated group of size $k$ to shift outcome $A$’s weight by $\Delta w$, they must manipulate comparisons involving $A$ across multiple pairs. With $m$ outcomes and random assignment, the number of comparisons needed is $O(m \cdot n / k)$. As $m$ and $n$ grow, the coordination cost scales super-linearly while the marginal impact diminishes. Statistical anomaly detection (e.g., comparing individual consistency ratios against population distributions) can identify coordinated patterns with high probability when $k < \sqrt{n}$.

Sybil Resistance: The incomplete information structure provides inherent Sybil resistance even beyond identity verification. A Sybil attack creating $k$ fake identities increases the attacker’s allocation power by factor $k$, but randomization spreads these fake votes across $O(m^2)$ possible pairs. The expected number of fake votes on any given pair remains $O(k/m^2)$, which is negligible when $k \ll m^2$. Combined with identity verification, this makes Sybil attacks both technically difficult and economically irrational.

Figure 3: The Sybil Dilution Effect. Even if a coordinated group of attackers creates fake accounts to target ‘Policy A’, the random assignment mechanism scatters their votes across the entire search space (Pairs X, Y, Z, etc.). The probability of any specific attacker being assigned the target pair is negligible, diluting the attack’s concentrated power.

6.4 Complexity of Real Policy Trade-offs

Criticism: Real policy decisions involve complex interdependencies, implementation constraints, and unintended consequences that citizens cannot evaluate.

Response: Wishocracy explicitly separates values (what we want) from implementation (how to achieve it). Citizens express preferences over outcomes (reduced cancer mortality, better schools, cleaner air) while experts design and evaluate implementation strategies. The service provider layer allows technical assessment of proposed solutions while keeping priority-setting in democratic hands. This division of labor matches citizens’ comparative advantage in welfare evaluation with experts’ advantage in causal analysis.

6.5 Legitimacy and Accountability

Criticism: Algorithmic aggregation lacks the transparency and accountability of representative institutions.

Response: The aggregation algorithm can be made fully transparent and auditable: open-source code, publicly verifiable inputs and outputs, and independent audits. This provides greater transparency than legislative logrolling and committee negotiations. Elected officials retain authority to override Wishocracy recommendations, but must publicly justify departures from expressed citizen preferences. This creates accountability in both directions: citizens to outcomes, and representatives to citizens.

6.6 Failure Modes and Robustness

Low Participation (<1%): When participation falls below critical thresholds, RAPPA faces two degradation modes. First, sampling bias emerges: if only 0.1% of citizens participate and they are systematically unrepresentative (e.g., only highly educated, politically engaged citizens), the aggregated preferences will not reflect population welfare. Second, comparison sparsity increases: with fewer participants, the pairwise comparison matrix becomes increasingly sparse, reducing the reliability of eigenvector estimates.

Mitigation: Statistical reweighting can correct for demographic bias, similar to survey research methods. Minimum participation thresholds can be enforced before outcomes become binding: if participation is below (e.g.) 2%, results are treated as advisory rather than binding. Adaptive incentives (entry into lotteries, public recognition) can boost participation. Empirical research suggests that pairwise comparison mechanisms achieve higher engagement than traditional surveys due to reduced cognitive load and increased perceived impact.

Low Comparison Density: As the number of policy priorities $m$ increases, the required comparisons grow quadratically ($O(m^2)$). With fixed participant budgets (each citizen completes $k$ comparisons), comparison density decreases as $k/m^2$. At very low densities ($k/m^2 < 0.01$), matrix completion methods may produce unstable estimates.

Mitigation: Hierarchical aggregation can reduce effective dimensionality by first aggregating within categories (Healthcare, Education, Defense), then across categories. Active sampling can prioritize comparisons with high uncertainty or inconsistency. Bayesian priors based on expert judgments or historical data can stabilize estimates in sparse regions. Empirical testing at wishocracy.org¹¹ suggests that convergence remains acceptable with as few as 3-5 comparisons per item, meaning systems with 100 priorities can function with ~300-500 comparisons per participant.

Coordinated Minority Attacks: A sophisticated attacker might coordinate a minority bloc to systematically manipulate outcomes. For example, 10% of voters might collude to always allocate 100% to priority $A$ in any comparison involving $A$, attempting to artificially inflate $A$’s priority weight.

Mitigation: Three defenses address this threat. (1) Dilution: With $n$ participants and random assignment, the coordinated bloc’s influence on any single comparison is $O(k/n)$ where $k$ is bloc size. As shown in Section 5.2, the marginal impact diminishes as $k/m^2$ when spread across all pairwise comparisons. (2) Statistical anomaly detection: Participants whose allocations are extreme outliers (always 100-0) across many comparisons can be flagged for review. If consistency ratios deviate beyond (e.g.) 3 standard deviations from population mean, weights can be downweighted. (3) Robustness analysis: Final allocations can be recomputed with suspected coordinated voters removed. If outcomes change dramatically (e.g., >20% shift in top priorities), this signals potential manipulation and triggers additional scrutiny.

Graceful Degradation: Critically, RAPPA degrades gracefully rather than catastrophically. Unlike binary voting where a 51-49 split produces winner-take-all outcomes, RAPPA with corrupted or sparse data still produces proportional allocations that approximate true preferences, albeit with increased noise. This property makes RAPPA suitable for pilot deployments where participation may initially be modest: the mechanism provides useful signals even before achieving full-scale adoption.

7 Implementation Pathway: From Information to Incentive Alignment

The most severe resource misallocations occur at the federal level: $886 billion annually on military spending versus $47 billion on the NIH, $20+ billion in fossil fuel subsidies, $50+ billion on drug war enforcement. Municipal discretionary budgets, while useful for proof-of-concept, represent rounding errors compared to the welfare losses from federal misallocation. We therefore propose a federal-first implementation strategy that begins with information provision and progresses toward incentive alignment with elected representatives.

7.1 Why Information Alone Fails: Politicians Respond to Incentives

Rankings of government programs by net societal value already exist and are systematically ignored. The Copenhagen Consensus has published rigorous benefit-cost analyses since 2004: childhood vaccinations (101:1 BCR), e-government procurement (125:1), maternal health interventions (87:1). These dramatically outperform military spending beyond deterrence requirements (~0.7:1 BCR) and fossil fuel subsidies (negative net societal value). GiveWell, Open Philanthropy, the IMF, and numerous academic institutions produce similar analyses.

Yet government spending patterns have not shifted.¹² analyzed 1,779 policy decisions and found that “economic elites and organized groups representing business interests have substantial independent impacts on U.S. government policy, while mass-based interest groups and average citizens have little or no independent influence.” The correlation between average citizen preferences and policy outcomes was effectively zero.

The marginal value of producing another ranking is zero. Politicians already know which programs produce net societal value. They don’t act on this knowledge because acting on it doesn’t appear in their utility function (reelection probability, campaign contributions, post-office career prospects). The solution is not more information but better incentives.

7.2 Three-Phase Implementation

7.2.1 Phase 1: Informational (Preference Gap Documentation)

Objective: Establish RAPPA as a credible measure of citizen preferences and document the gap between public preferences and actual federal allocations.

Mechanism:

Deploy RAPPA on major federal budget categories (Defense, Healthcare, Education, Infrastructure, Research, Social Services, etc.)
Aggregate preferences from a statistically representative sample of U.S. adults
Publish annual “Preference Gap Report” showing divergence between RAPPA allocations and actual federal budget
Generate media attention around largest divergences (e.g., “Citizens would allocate 3x more to medical research and 40% less to military”)

Success Metrics:

Metric	Target
Participants	100,000+ annually
Demographic representativeness	Within 5% of census on key demographics
Preference stability (year-over-year)	τ ≥ 0.8
Media coverage	Major outlet coverage of Preference Gap Report

Timeline: 12-18 months to establish credibility and baseline measurements.

Why this works: Information alone won’t change policy, but it creates the foundation for Phase 2. The Preference Gap Report becomes a political tool: candidates can campaign on “aligning with citizen preferences” and opponents can be attacked for “ignoring what voters actually want.”

7.2.2 Phase 2: Accountability Scoring (Politician Alignment Ratings)

Objective: Create a public scoring system that rates elected officials based on how their voting records correlate with RAPPA-expressed citizen preferences.

Mechanism:

Map each congressional vote to affected budget categories
Calculate alignment score: correlation between politician’s voting pattern and RAPPA preference weights
Publish “Citizen Alignment Scores” for all members of Congress
Update scores in real-time as new votes occur

Scoring Formula:

For politician $p$ with voting record $\mathbf{v}_p$ across $k$ budget-relevant votes, and RAPPA preference vector $\mathbf{w}$:

\[ \text{AlignmentScore}_p = \frac{\mathbf{v}_p \cdot \mathbf{w}}{|\mathbf{v}_p||\mathbf{w}|} \]

where votes are coded as +1 (increases funding for category), -1 (decreases funding), or 0 (neutral).

Success Metrics:

Metric	Target
Vote coverage	>80% of budget-relevant votes mapped
Score volatility	Stable rankings (τ ≥ 0.9 month-over-month)
Politician awareness	>50% of Congress aware of their score
Electoral salience	Alignment scores cited in >10% of competitive races

Timeline: 6-12 months after Phase 1 baseline established.

Why this works: Politicians are highly sensitive to public ratings. The NRA’s letter grades, the League of Conservation Voters’ scorecard, and similar systems demonstrably influence politician behavior. A “Citizen Alignment Score” backed by transparent methodology and large sample sizes becomes a powerful accountability tool.

7.2.3 Phase 3: Incentive Alignment (Integration with Incentive Alignment Bonds)

Objective: Channel financial and electoral resources to politicians based on their alignment with citizen preferences, making welfare-improving votes incentive-compatible.

Mechanism:

Wishocracy’s preference aggregation integrates with Incentive Alignment Bonds (IABs), a mechanism design approach to political economy. IABs create three layers of incentive alignment:

Electoral Layer: Campaign contributions, endorsements, and volunteer mobilization flow to high-alignment politicians. A PAC or 501(c)(4) aggregates small-dollar donations from citizens and allocates them proportionally to Citizen Alignment Scores.
Scoring Layer: The RAPPA-based Citizen Alignment Score provides the objective function that IABs optimize. Unlike traditional interest group scores (which reflect narrow priorities), RAPPA scores reflect aggregated citizen welfare preferences.
Post-Office Layer: High-alignment politicians gain access to lucrative post-office opportunities (board seats, consulting, foundation positions) funded by IAB investors who profit from welfare-improving policy adoption.

Politicians currently face incentives that reward serving concentrated interests (military contractors, pharmaceutical incumbents, fossil fuel producers) at the expense of diffuse beneficiaries (citizens who would benefit from cures, climate stability, reduced existential risk). IABs flip this calculus by making the diffuse beneficiaries’ preferences financially consequential.

Capital Asymmetry: Diffuse beneficiaries collectively control far more capital than concentrated interests. Global household wealth exceeds $454T; the combined market capitalization of industries benefiting from misallocation (defense contractors, fossil fuels, etc.) is under $5T. The problem is coordination, not resources. IABs solve the coordination problem by creating a vehicle for diffuse beneficiaries to pool resources and direct them toward aligned politicians.

Success Metrics:

Metric	Target
PAC funding	$10M+ in first electoral cycle
Alignment score correlation with contributions	r ≥ 0.7
Electoral outcomes	High-alignment candidates win at higher rates than low-alignment
Policy shift	Measurable movement toward RAPPA preferences in appropriations

Timeline: 2-4 years after Phase 2 establishes credible scoring system.

7.3 Why Federal-First Beats Municipal Pilots

Dimension	Municipal Pilot	Federal Implementation
Misallocation at stake	$1-10M	$500B+ annually
Welfare impact	Marginal	Transformative
Legal barriers	Requires municipal buy-in	Information/scoring requires no government cooperation
Scalability	Must replicate across 1000s of municipalities	Single implementation covers entire federal budget
Media attention	Local coverage	National/international coverage
Incentive alignment	Limited (council members face weak incentives)	High (members of Congress highly sensitive to scores and contributions)

The municipal approach treats Wishocracy as a replacement for representative democracy, requiring politicians to cede authority. The federal approach treats Wishocracy as an accountability mechanism that makes representative democracy work better, requiring no authority transfer, only information provision and incentive alignment.

7.4 Evaluation Framework

Despite the federal focus, rigorous evaluation remains essential:

7.4.1 Preference Aggregation Quality

Metric	Measurement	Success Threshold
Test-retest reliability	Correlation on repeated pairs	r ≥ 0.7
Aggregate stability	Year-over-year rank correlation	τ ≥ 0.8
Demographic representativeness	Comparison to census	No significant difference
Manipulation resistance	Robustness to outlier removal	<5% shift in top priorities

7.4.2 Accountability System Effectiveness

Metric	Measurement	Success Threshold
Score predictive validity	Correlation between alignment score and future votes	r ≥ 0.6
Electoral salience	Candidates referencing alignment scores	>10% of competitive races
Behavioral response	Politicians shifting votes after score publication	Measurable movement

7.4.3 Incentive Alignment Impact

Metric	Measurement	Success Threshold
Contribution-alignment correlation	PAC dollars vs. alignment score	r ≥ 0.7
Electoral outcomes	Win rate by alignment quintile	Positive gradient
Policy outcomes	Appropriations shift toward RAPPA preferences	Measurable movement
Preference gap reduction	Year-over-year change in divergence	Decreasing trend

7.5 Connection to Incentive Alignment Bonds

Wishocracy and Incentive Alignment Bonds are complementary mechanisms addressing different parts of the democratic failure:

Wishocracy (RAPPA) solves the preference aggregation problem: How do we know what citizens actually want across complex, multidimensional policy spaces?
Incentive Alignment Bonds solve the incentive alignment problem: How do we make politicians act on citizen preferences rather than concentrated interests?

Together, they form a complete system: RAPPA provides the objective function (what to optimize for), and IABs provide the optimization pressure (why politicians should care). Neither mechanism alone is sufficient: information without incentives produces ignored reports; incentives without information produces captured allocation.

For detailed treatment of the IAB mechanism, including formal models, legal analysis, and bootstrap strategy, see the companion paper: Incentive Alignment Bonds: A Mechanism Design Approach to Political Economy.

7.6 Connection to Optimocracy

Wishocracy and Optimocracy represent two distinct approaches to governance reform that can function independently or in combination:

Wishocracy is democratic: citizens express preferences, and the mechanism aggregates them. The output is a preference signal that politicians can choose to follow or ignore (absent incentive mechanisms).
Optimocracy is algorithmic: a pre-agreed metric is optimized automatically, with minimal human discretion. The output is an allocation that executes regardless of political preferences.

These approaches address different failure modes:

Failure Mode	Wishocracy Solution	Optimocracy Solution
Preference aggregation	RAPPA pairwise comparison	N/A (metric pre-selected)
Capture by interests	Accountability scores	Remove human discretion
Time-inconsistency	Continuous measurement	Algorithmic commitment
Metric gaming (Goodhart)	Adapts to changing preferences	Vulnerable
Democratic legitimacy	High (citizen input)	Lower (algorithm decides)

A hybrid architecture might use Wishocracy for metric selection (citizens choose what to optimize) and Optimocracy for metric optimization (algorithms allocate to maximize the chosen metric). This combines democratic legitimacy at the constitutional level with capture resistance at the execution level.

For detailed treatment of algorithmic governance, including smart contract specifications and oracle design, see the companion paper: Optimocracy: Algorithmic Governance Through Metric-Bound Resource Allocation.

8 Conclusion

Representative democracy’s principal-agent problem is not a bug but a structural feature: elected officials inevitably face incentives that diverge from citizen welfare. No amount of campaign finance reform, term limits, or transparency requirements can eliminate the fundamental misalignment between representatives who must satisfy donors and constituents simultaneously. Meanwhile, direct democracy mechanisms remain cognitively infeasible for the complex, multidimensional trade-offs that characterize modern governance.

Wishocracy offers a different approach: rather than replacing representatives, align their incentives with citizen preferences. Through Randomized Aggregated Pairwise Preference Allocation, the mechanism aggregates citizen preferences into a clear signal of what voters actually want. Combined with Citizen Alignment Scores and Incentive Alignment Bonds, this creates accountability pressure that makes welfare-improving votes politically and financially rewarding. The theoretical foundations combine the Analytic Hierarchy Process (for cognitive tractability) with collective intelligence research (for aggregation), decomposing n-dimensional preference spaces into simple pairwise comparisons that any citizen can complete.

The empirical precedents from Porto Alegre’s participatory budgeting, Taiwan’s vTaiwan platform, and Stanford’s voting research demonstrate that citizens can and will engage productively with pairwise preference-expressing mechanisms. These real-world experiments validate the core assumptions underlying Wishocracy while revealing the institutional fragility of advisory mechanisms that lack connection to electoral incentives.

Several questions require further research. First, what is the minimum sample size and comparison density needed for preference convergence across different problem domains? Second, how does preference stability vary with issue complexity and temporal distance? Third, what scoring methodologies best capture alignment between voting records and citizen preferences? Fourth, how can the mechanism be adapted for parliamentary systems, multi-party democracies, and other institutional contexts beyond the U.S. Congress?

The mechanism design presented here represents one point in a broader design space of democratic innovations. Alternative aggregation methods (Bradley-Terry models, Bayesian updating, deep learning approaches), different elicitation formats (rating scales, probability distributions, stochastic choice), and various institutional embeddings (legislative priority-setting, constitutional conventions, international treaty negotiations) warrant systematic exploration.

Wishocracy addresses the central failure mode of democratic governance: the principal-agent problem that corrupts representative institutions. The mechanism combines four elements: AHP’s cognitive tractability, slider-based preference intensity capture, collective intelligence aggregation, and (critically) integration with incentive mechanisms that make representatives care about alignment scores. Information alone changes nothing. Information plus incentives can change everything.

The mechanism is implementable with current technology, grounded in validated theory, and supported by empirical precedents. A reference implementation is available at wishocracy.org for public testing and audit. Whether Wishocracy can achieve its theoretical promise (truly aligning public resource allocation with citizen welfare) remains an open empirical question that only real-world deployment can answer.

9 Appendix A: The Service Provider Layer

Important: Service providers represent a distinct, separate layer from the core RAPPA mechanism. While RAPPA handles democratic preference aggregation to determine what society should prioritize, service providers address the orthogonal question of how to achieve those priorities.

Once priorities are established through RAPPA, Wishocracy introduces this second layer for solution generation and evaluation. Service providers (which may include government agencies, private contractors, NGOs, or other qualified entities) form around specific priorities to propose implementation strategies. These proposals are subject to pairwise comparison using different evaluation criteria: cost-effectiveness, feasibility, and probability of success.

This two-layer architecture embodies a fundamental division of labor:

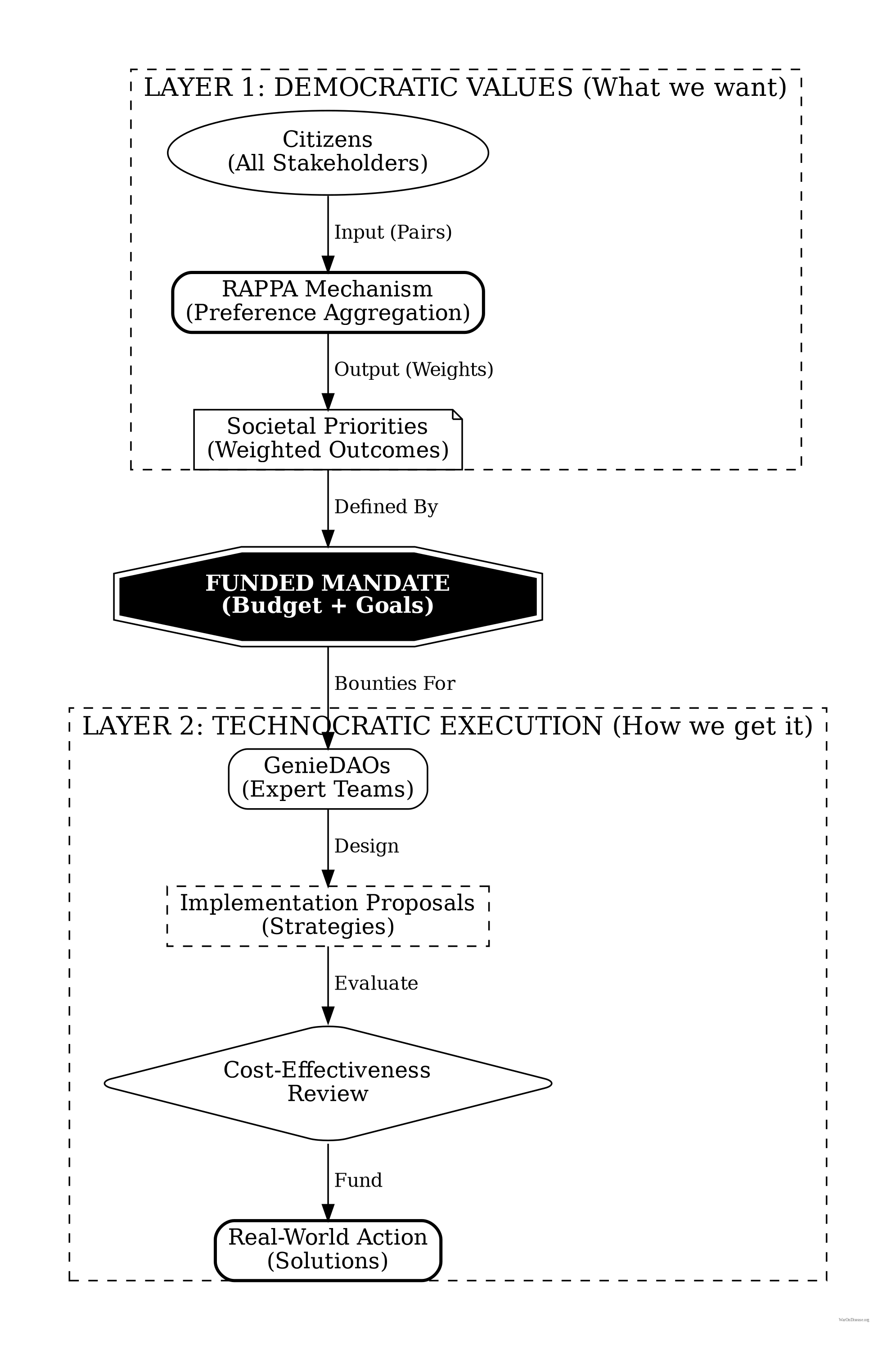
Layer 1 (RAPPA): Democratic, values-based. “What should we do?” Citizens express preferences over outcomes (reduced cancer mortality, better schools, cleaner air) based on their welfare valuations.
Layer 2 (Service Providers): Technocratic, evidence-based. “How should we do it?” Experts design and evaluate implementation strategies based on causal knowledge and empirical evidence.

This separation addresses a key criticism of technocracy (experts shouldn’t determine societal values) while respecting the limits of direct democracy (citizens cannot evaluate complex implementation trade-offs). Each layer operates where its participants have comparative advantage: citizens in welfare evaluation, experts in causal analysis.

References

Suisse/UBS, C. Credit suisse global wealth report 2023. Credit Suisse/UBS https://www.ubs.com/global/en/family-office-uhnw/reports/global-wealth-report-2023.html (2023)

Total global household wealth: USD 454.4 trillion (2022) Wealth declined by USD 11.3 trillion (-2.4%) in 2022, first decline since 2008 Wealth per adult: USD 84,718 Additional sources: https://www.ubs.com/global/en/family-office-uhnw/reports/global-wealth-report-2023.html

Saaty, T. L. The Analytic Hierarchy Process. (Saaty, 1980).

The foundational text on the Analytic Hierarchy Process (AHP) methodology for decision-making. AHP decomposes complex decisions into hierarchies of criteria and sub-criteria, then elicits pairwise comparisons at each level. For n alternatives, this requires only n(n-1)/2 comparisons rather than the cognitively impossible simultaneous comparison of all n options. The pairwise comparison matrices are then synthesized using eigenvector methods to produce consistent priority rankings. Additional sources: https://archive.org/details/analytichierarch0000saat | https://books.google.com/books/about/The_Analytic_Hierarchy_Process.html?id=Xxi7AAAAIAAJ | https://link.springer.com/chapter/10.1007/978-1-4613-2805-6_12

Surowiecki, J. The Wisdom of Crowds. (Surowiecki, 2004).

Explores the aggregation of information in groups, arguing that decisions are often better than could have been made by any single member of the group. The opening anecdote relates Francis Galton’s surprise that the crowd at a county fair accurately guessed the weight of an ox when the median of their individual guesses was taken. The three conditions for a group to be intelligent are diversity, independence, and decentralization. Additional sources: https://archive.org/details/wisdomofcrowds0000suro | https://en.wikipedia.org/wiki/The_Wisdom_of_Crowds | https://www.amazon.com/Wisdom-Crowds-James-Surowiecki/dp/0385721706

Miller, G. A. Cognitive limit in short-term memory (miller’s law). George A. Miller https://doi.org/10.1037/h0043158 (1956)

Short-term memory capacity: 7 ± 2 items (Miller’s Law) The "magical number seven" - humans can hold approximately 7 chunks of information in working memory Note: This classic psychology paper has been cited over 40,000 times and fundamentally shaped our understanding of human cognitive limitations Additional sources: https://doi.org/10.1037/h0043158

Saaty, T. L. Decision making with the analytic hierarchy process. Saaty 1, 83–98 (2008)

Decisions involve many intangibles that need to be traded off. To do that, they have to be measured along side tangibles whose measurements must also be evaluated as to, how well, they serve the objectives of the decision maker. The Analytic Hierarchy Process (AHP) is a theory of measurement through pairwise comparisons and relies on the judgements of experts to derive priority scales. This paper has been cited 9,181 times, with 1,042 highly influential citations. Additional sources: https://www.inderscienceonline.com/doi/abs/10.1504/IJSSci.2008.01759 | https://www.semanticscholar.org/paper/DECISION-MAKING-WITH-THE-ANALYTIC-HIERARCHY-PROCESS-Saaty/e3c561049eb532e328fc2b8288c490986cd9403f | https://www.researchgate.net/publication/228628807_Decision_making_with_the_Analytic_Hierarchy_Process

Lalley, S. P. & Weyl, E. G. Quadratic voting: How mechanism design can radicalize democracy. Lalley 108, 33–37 (2018)

The paper proposes a design where individuals pay for as many votes as they wish using a number of "voice credits" in the votes they buy. Only quadratic cost induces marginal costs linear in votes purchased and thus welfare optimality if individuals’ valuation of votes is proportional to their value of changing the outcome. Additional sources: https://www.aeaweb.org/articles?id=10.1257/pandp.20181002 | https://ssrn.com/abstract=2003531 | https://www.microsoft.com/en-us/research/publication/quadratic-voting-how-mechanism-design-can-radicalize-democracy/

Rebecca Abers, R. K., Igor Brandão & Votto, D. Porto alegre: Participatory budgeting and the challenge of sustaining transformative change. (2018)

Examines transformative urban change in Porto Alegre, Brazil, through the lens of participatory budgeting. However, political support for participatory budgeting in its birthplace has declined through the years, culminating in its suspension in Porto Alegre in 2017. The success of participatory budgeting as a tool of transformative urban change is contingent on four conditions: (1) well-structured participatory arrangements to ensure participation from a wide range of actors across society; (2) adequate financial resources; (3) political commitment and flexibility to adjust to changing political realities; and (4) government commitment to implement the proposals the process generates. Additional sources: https://www.wri.org/research/porto-alegre-participatory-budgeting-and-challenge-sustaining-transformative-change | https://www.oidp.net/docs/repo/doc415.pdf

Cabannes, Y. Participatory budgeting: A significant contribution to participatory democracy. Cabannes 16, 27–46 (2004)

This paper describes participatory budgeting in Brazil and elsewhere as a significant area of innovation in democracy and local development. It draws on the experience of 25 municipalities in Latin America and Europe, selected based on the diversity of their participatory budgeting experience and their degree of innovation. Additional sources: https://www.iied.org/g00471 | https://www.researchgate.net/publication/32893674_Participatory_Budgeting_A_Significant_Contribution_to_Participatory_Democracy

Joshua C. Yang, D. P., Carina I. Hausladen & Helbing, D. Designing digital voting systems for citizens: Achieving fairness and legitimacy in participatory budgeting. Yang 5, 1–30 (2024)

Identifies approaches to designing participatory budgeting voting that minimize cognitive load and enhance the perceived fairness and legitimacy of the digital process from the citizens’ perspective. Main results: participants preferred voting input formats that are more expressive (like rankings and distributing points) over simpler formats (like approval voting); participants indicated a desire for the budget to be fairly distributed across city districts and project categories; participants found the Method of Equal Shares voting rule to be fairer than the conventional Greedy voting rule. Additional sources: https://dl.acm.org/doi/10.1145/3665332 | https://arxiv.org/abs/2310.03501 | https://www.researchgate.net/publication/380771947_Designing_Digital_Voting_Systems_for_Citizens_Achieving_Fairness_and_Legitimacy_in_Participatory_Budgeting

10.

Aczél, J. & Saaty, T. L. Procedures for synthesizing ratio judgements. Journal of Mathematical Psychology 27, 93–102 (1983).

11.

Wishonia. Wishocracy: A decentralized semi-autonomous todo list for humanity. (2024).

12.

Gilens, M. & Page, B. I. Testing theories of american politics: Elites, interest groups, and average citizens. Perspectives on Politics 12, 564–581 (2014).

13.

Downs, A. An Economic Theory of Democracy. (Harper & Row, 1957).

14.

Rawls, J. A Theory of Justice. (Harvard University Press, 1971).

15.

Wellings, T. et al. Fair and inclusive participatory budgeting: Voter experience with cumulative and quadratic voting interfaces. in vol. 14536 65–71 (2024).

Cumulative and quadratic voting are two distributional voting methods that are expressive, promoting fairness and inclusion in participatory budgeting. This paper introduces an implementation and evaluation of cumulative and quadratic voting within Stanford Participatory Budgeting. While voters prefer simple methods, the more expressive (and complex) cumulative voting becomes the preferred one compared to k-ranking voting that is simpler but less expressive. Additional sources: https://link.springer.com/chapter/10.1007/978-3-031-61698-3_6 | https://arxiv.org/abs/2308.04345 | https://www.researchgate.net/publication/372990037_Fair_and_Inclusive_Participatory_Budgeting_Voter_Experience_with_Cumulative_and_Quadratic_Voting_Interfaces

Reuse

CC BY-NC 4.0

1 Abstract

2 Introduction: The Preference Aggregation Problem

3 Theoretical Foundations

3.1 The Analytic Hierarchy Process

3.2 The Preference Intensity Problem

3.3 Collective Intelligence and the Wisdom of Crowds

3.4 Related Work and Positioning in the Literature

4 Mechanism Design: Randomized Aggregated Pairwise Preference Allocation

4.1 Core Mechanism

4.1.1 Scenario: Federal Budget Preferences

4.2 Formal Properties

4.3 Formal Model

4.4 Computational Complexity and Scalability

4.5 Comparative Information & Welfare Analysis

4.5.1 Information-Theoretic Superiority

4.5.2 Welfare Maximization: The “Median vs. Mean” Proof

4.5.3 Principal-Agent Cost Elimination

5 Empirical Precedents and Evidence Base

5.1 Porto Alegre Participatory Budgeting

5.2 Taiwan’s Digital Democracy Experiments

5.3 Stanford Participatory Budgeting Platform Research

5.4 Colorado Quadratic Voting Experiment

5.5 Reference Implementation: Wishocracy.org

5.5.1 Category Selection and Validation Methodology

5.5.2 Zero-Funding Filter Optimization

5.5.3 Hierarchical Category Structure

5.5.4 Framing Bias and Mitigation

6 Addressing Potential Criticisms

6.1 Participation and Digital Divide

6.2 Manipulation and Sybil Attacks

6.3 Preference Laundering and Manufactured Consent

6.4 Complexity of Real Policy Trade-offs

6.5 Legitimacy and Accountability

6.6 Failure Modes and Robustness

7 Implementation Pathway: From Information to Incentive Alignment

7.1 Why Information Alone Fails: Politicians Respond to Incentives

7.2 Three-Phase Implementation

7.2.1 Phase 1: Informational (Preference Gap Documentation)

7.2.2 Phase 2: Accountability Scoring (Politician Alignment Ratings)

7.2.3 Phase 3: Incentive Alignment (Integration with Incentive Alignment Bonds)

7.3 Why Federal-First Beats Municipal Pilots

7.4 Evaluation Framework

7.4.1 Preference Aggregation Quality

7.4.2 Accountability System Effectiveness

7.4.3 Incentive Alignment Impact

7.5 Connection to Incentive Alignment Bonds

7.6 Connection to Optimocracy

8 Conclusion

9 Appendix A: The Service Provider Layer

References

Reuse

Copyright